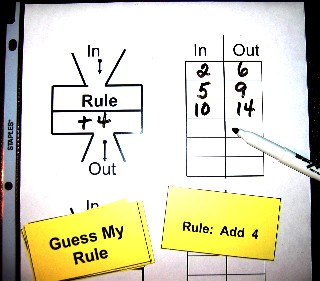
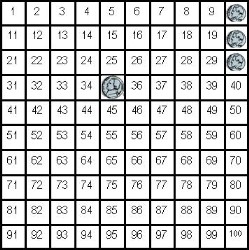
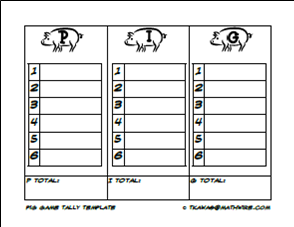
Older students will practice coordinate graphing skills as they play Catch the Gingerbread Man, a Battleship-type game where students try to capture their opponent's gingerbread men.
Younger students will enjoy the Run, Gingerbread Man, Run! game which comes with a colored spinner, gameboard and directions for small group play. Students will practice simple counting skills as they try to be the first to move through the colored board.
Students may use a copy of the gameboard to analyze the results of winners:
- Did the red, yellow, blue or green gingerbread man win more often?
- Does each color have an equal chance of winning? Explain your thinking
Problem solving activities involve combinations. Gingerbread Bake Sale challenges students to figure out if Ruby can make each of the 12 gingerbread cookies on a cookie sheet different, given the possible eyes and noses. Gingerbread Man Combinations is a harder version of this problem, with more choices to challenge older students. Gingerbread Man Chain requires students to use measurement skills to figure out how many gingerbread men will be needed to create borders at the top and bottom of a bulletin board.