Lattice Multiplication

This algorithm works well for students who are developing multiplication fact fluency. Students may begin using a template to solve multiplication problems, but they quickly learn to draw their own lattice matrix to solve problems. Students love the method and it is very successful with both whole numbers and decimals. Teach students this multiplication algorithm as one of many different algorithms they may elect to use.  Students will very quickly learn to multiply large numbers, using basic multiplication facts and addition/regrouping skills.

Procedure:

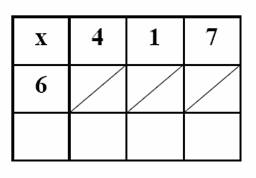
• Student writes the problem in the grid (e.g. 6 x 417).
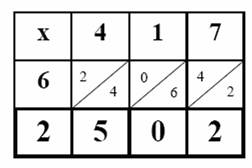
• Student then writes the answer to each single digit multiplication in the appropriate square.
• The tens digit is placed above the diagonal; the ones digit below the diagonal.
• When all squares have been completed, the student sums the numbers between each set of diagonals, and writes the sum at the bottom of the grid. NOTE: If the sum is greater than 10, regroup the ten to the next diagonal to the left.
• The student can now simply read the answer from left to right and insert commas, as appropriate.

For a complete overview of this method, see Cool Math's explanation of Lattice Multiplication to view the step-by-step procedure.  Take a cue from the site's explanation and use colored markers when introducing this algorithm to students on the overhead or whiteboard.  

Practice:

• Download Lattice Multiplication for a practice page.
• Download Lattice Multiplication Answers for answers to the practice page.

Templates:   Three different templates are included for Lattice Multiplications.   Templates are designed to be used in sheet protectors.   This strategy allows students to use dry-erase markers and re-use the same paper for many multiplication problems.

• Download the Lattice grids for a single digit multiplier.
• Download the Lattice grid for a 2-digit multiplier.
• Download the Lattice grid for 2-3 digit multipliers.